一致性 Hash 原理及 GroupCache 源码分析
一致性 Hash 常用于缓解分布式缓存系统扩缩容节点时造成的缓存大量失效的问题。一致性 Hash 与其说是一种 Hash 算法,其实更像是一种负载均衡策略。
GroupCache 是 golang 官方提供的一个分布式缓存库,其中包含了一个简单的一致性 Hash 的实现。其代码在 github.com/golang/groupcache/consistenthash。本文将会基于 GroupCache 的一致性 Hash 实现,深入剖析一致性 Hash 的原理。
本文会着重探讨以下几点内容:
- 传统的 Hash 式负载均衡在集群扩缩容时面临的缓存失效问题。
- 一致性 Hash 的原理。
- Golang 的开源库 GroupCache 如何实现一致性 Hash。
集群扩缩容导致缓存的问题
我们先看下传统的 Hash 式负载均衡,当集群扩缩容时会遇到哪些问题。
假设我们有三台缓存服务器,每台服务器用于缓存一部分用户的信息。最常见的 Hash 式负载均衡做法是:对于指定用户,我们可以对其用户名或者其他唯一信息计算 hash 值,然后将该 hash 值对 3 取余,得到该用户对应的缓存服务器。如下图所示:
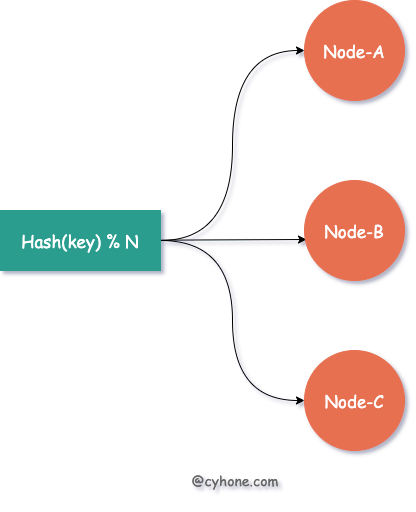
而当我们需要对集群进行扩容或者缩容时,增加或者减少部分服务器节点,将会带来大面积的缓存失效。
例如需要扩容一台服务器,即由 3 台缓存服务器增加为 4 台,那么之前 hash(username) % 3 这种策略,将变更为 hash(username) % 4。整个负载均衡的策略发生了彻底的变化,对于任何一个用户都会面临Hash失效的风险。
而一旦缓存集体失效,所有请求无法命中缓存,直接打到后端服务上,系统很有可能发生崩溃。
一致性 Hash 的原理
针对以上问题,如果使用一致性 Hash 作为缓存系统的负载均衡策略,可以有效缓解集群扩缩容带来的缓存失效问题。
相比于直接对 hash 取模得到目标 Server 的做法,一致性 Hash 采用 有序 Hash 环 的方式选择目标缓存 Server。如下图所示:
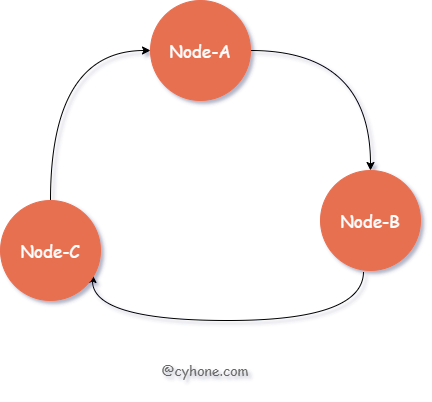
对于该有序 Hash 环,环中的每个节点对应于一台缓存 Server,同时每个节点也包含一个整数值。各节点按照该整数值从小到大依次排列。
对于指定用户来说,我们依然首先出计算用户名的 hash 值。接着,在 Hash 环中按照值大小顺序,从小到大依次寻找,找到 第一个大于等于该 hash 值的节点,将其作为目标缓存 Server。
例如,我们 hash 环中的三个节点 Node-A、Node-B、Node-C 的值依次为 3、7、13。假设对于某个用户来说,我们计算得到其用户名的 hash 值为 9,环中第一个大于 9 的节点为 Node-C,则选用 Node-C 作为该用户的缓存 Server。
缓存失效的缓解
以上就是正常情况下一致性 Hash 的使用,接下来我们看下,一致性 Hash 是如何应对集群的扩缩容的。
当我们对集群进行扩容,新增一个节点 New-Node, 假设该节点的值为 11。那么新的有序 Hash 环如下图所示:
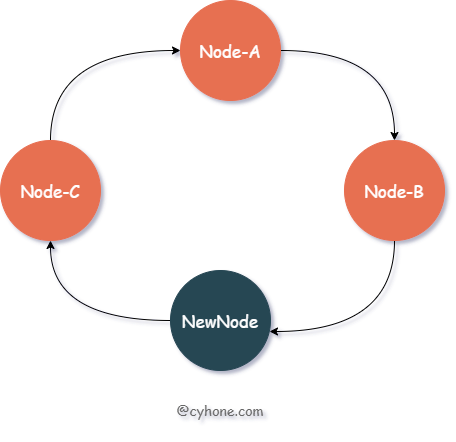
我们看下此时的缓存失效情况:在这种情况下, 只会造成 hash 值范围在 Node-B 和 NewNode 之间(即(7, 11])的数据缓存失效。这部分数据原本分配到节点 Node-C(值为 13),现在都需要迁移到新节点 NewNode 上。
而原本分配到 Node-A、Node-B 两个节点上的缓存数据,不会受到任何影响。之前值范围在 NewNode 和 Node-B 之间(即(11, 13])的数据,被分配到了 Node-C 上面。新节点出现后,这部分数据依然属于 Node-C,也不会受到任何影响。
一致性 Hash 利用有序 Hash 环,巧妙的缓解了集群扩缩容造成的缓存失效问题。注意,这里说的是 “缓解”,缓存失效问题无法完全避免,但是可以将其影响降到最低。
这里有个小问题是,因为有序 Hash 环需要其中每个节点有持有一个整数值,那这个整数值如何得到呢?一般做法是,我们可以利用该节点的特有信息计算其 Hash 值得到, 例如 hash(ip:port)。
数据倾斜与虚拟节点
以上介绍了一致性 hash 的基本过程,这么看来,一致性 hash 作为缓解缓存失效的手段,的确是行之有效的。
但我们考虑一个极限情况,假设整个集群就两个缓存节点: Node-A 和 Node-B。则 Node-B 中将存放 Hash 值范围在 (Node-A, Node-B] 之间的数据。而 Node-A 将承担两部分的数据: hash < Node-A 和 hash > Node-B。
从这个值范围,我们可以轻易的看出,Node-A 的值空间实际上远大于 Node-B。当数据量较大时,Node-A 承担的数据也将远超于 Node-B。实际上,当节点过少时,很容易出现分配给某个节点的数据远大于其他节点。这种现象我们往往称之为 “数据倾斜”。
对于此类问题,我们可以引入虚拟节点的概念,或者说是副本节点。每个真实的缓存 Server 在 Hash 环上都对应多个虚拟节点。如下图所示:

对于上图来说,我们其实依然只有三个缓存 Server。但是每个 Server 都有一个副本,例如 V-Node-A 和 Node-A 都对应同一个缓存 Server。
GroupCache 的一致性 Hash 实现
GroupCache 提供了一个简单的一致性 hash 的实现。其代码在 github.com/golang/groupcache/consistenthash。
我们先看下它的使用方法:
1 | import ( |
consistenthash 对外提供了三个函数:
New(replicas int, fn Hash):构造一个 consistenthash 对象,replicas代表每个节点的虚拟节点个数,例如 replicas 等于 3,代表每个节点在 Hash 环上都对应有三个虚拟节点。fn代表自定义的 hash 函数,传 nil 则将会使用默认的 hash 函数。Add函数:向 Hash 环上添加节点。Get函数:传入一个 key,得到其被分配到的节点。
Add 函数
我们先看下其 Add 函数的实现。Add 函数用于向 Hash 环上添加节点。其源码如下:
1 | func (m *Map) Add(keys ...string) { |
在 Add 函数里面涉及两个重要的属性:
- keys: 类型为
[]int。这个其实就是我们上面说的有序 Hash 环,这里用了一个数组表示。数组中的每一项都代表一个虚拟节点以及它的值。 - hashMap:类型为
map[int]string。这个就是虚拟节点到用户传的真实节点的映射。map 的 key 就是keys属性的元素。
在这个函数里面有生成虚拟节点的操作。例如用户传了真实节点为 ["Node-A", "Node-B"], 同时 replicas 等于 2。则 Node-A 会对应 Hash 环上两个虚拟节点:0Node-A,1Node-A,这两个节点对应的值也是直接进行对其计算 hash 得到。
需要注意的是,每次 Add 时候,函数最后会对 keys 进行排序。因此最好一次把所有的节点都加进来,以避免多次排序。
Get 函数
接下来我们分析下 Get 函数的使用,Get 函数用于给指定 key 分配对应节点。其源码如下:
1 | func (m *Map) Get(key string) string { |
首先计算用户传的 key 的 hash 值,然后利用 sort.Search 在 keys 中二分查找,得到数组中满足情况的最小值。因为 keys 是有序数组, 所以使用二分查找可以加快查询速度。
如果没有找到则使用首元素,这个就是环形数组的基本操作了。最后利用 hashMap[keys[idx]], 由虚拟节点,得到其真实的节点。
以上就是 Groupcache 对一致性 Hash 的实现了。这个实现简单有效,可以帮助我们快速理解一致性 Hash 的原理。